Who is Doing the Talking in Math Class?
When to Use Direct Instruction in a Thinking Classroom.
As a teacher, I am continually thinking about when I should talk and when I should listen. Early in my teaching career I believed that the type of textbook dictated who was talking in my classroom. I started my career teaching with a problem-based curriculum, which meant students solved problems together by talking to each other and my job was to walk around the classroom listening to the conversations and then use what I heard to lead a class discussion.
My struggle while teaching with this approach was deciding when and what to talk about. I didn’t want to tell students too much and take away their thinking. At the same time, I felt the need to talk and show examples since that is what my teachers did when I was in school.
Later in my career, my school adopted a more traditional textbook and my role as a teacher changed. The book was full of examples so I would talk for most of the hour as I worked out examples in front the class as my students listened and vigorously copied the examples onto their notes.
My struggle with this approach was finding ways to help students talk about their ideas and explain their thinking. I knew if I talked too much, my students would stop listening.
Recently, I have found some answers by digging into different types of instruction. Munster, Stein, and Smith (2015b)1 define two types of instruction: dialogic and direct.
In the direct instruction model, when students have the prerequisite conceptual and procedural knowledge, they will learn from (a) watching clear, complete demonstrations of how to solve problems, with accompanying explanations and accurate definitions; (b) practicing similar problems sequenced according to difficulty; and (c) receiving immediate, corrective feedback.
Whereas in the dialogic model, students must (a) actively engage in new mathematics, persevering to solve novel problems; (b) participate in a discourse of conjecture, explanation, and argumentation; (c) engage in generalization and abstraction, developing efficient problem solving strategies and relating their ideas to conventional procedures; and to achieve fluency with these skills, (d) engage in some amount of practice. (p6)
For simplicity, let's say that these two models relate to who is doing the talking. In direct instruction, the teacher is doing the majority of the talking while in dialogic instruction the talking is done by the students.
In the book Visible learning for Mathematics, Hattie, Fisher, and Frey (p 24)2 discuss the effect of each of these types of instruction. Stating that direct instruction has an effect size of 0.59 and dialogic instruction has an effect size of 0.82. These authors encourage teachers not to choose one method over the other but to choose which method is best for the situation.
I saw positive results with dialogic instruction early in my teaching career when teaching a problem-based curriculum and wanted to incorporate this model again. So three years ago, I started implementing the practices of Building Thinking Classrooms (BTC). What immediately drew me to these practices was the ability to change traditional “show and tell” examples into thinking tasks. I write about how I did this in the article Building a Thinking Classroom with a Traditional Textbook and students now do the thinking and the majority of the talking in my class.
While dialogic instruction yields a high effect size, it does not always reach all students. As much as I enjoy hearing students discussing math, at some point I need to talk to the class; either to verify that their thinking is correct, to fill in any missing pieces, or take care of misconceptions. Which is why I incorporate both types of instruction in my lessons.
Dialogic Instruction
All lessons start with dialogic instruction. Students can’t explore and engage in new mathematics if they have first been shown how to solve the problems. In BTC, this happens when students are working on thinking problems at the whiteboards. Here, students discuss the problems together and develop conceptual understanding of how to solve them. During this time, I am listening to student discussions to help me offer the proper hints and extensions to each group. I’m also listening for different approaches to solving problems and common misconceptions.
Direct Instruction
Direct instruction comes after students have time to make their own generalizations and evaluate their conjectures. Students need to leave class being sure that they know what they are supposed to know. To do this, I choose a problem that encompasses the learning goal, and we solve it together. Students tell me what to write down and they include this example in their notes. This is a form of direct instruction, but in this case, the students are instructing me, and by writing down their thoughts, I am confirming their thinking. I also use this time to highlight student work by pointing out different strategies and addressing any misconceptions. I write about this in more depth in the article The Power of Consolidating a Lesson.
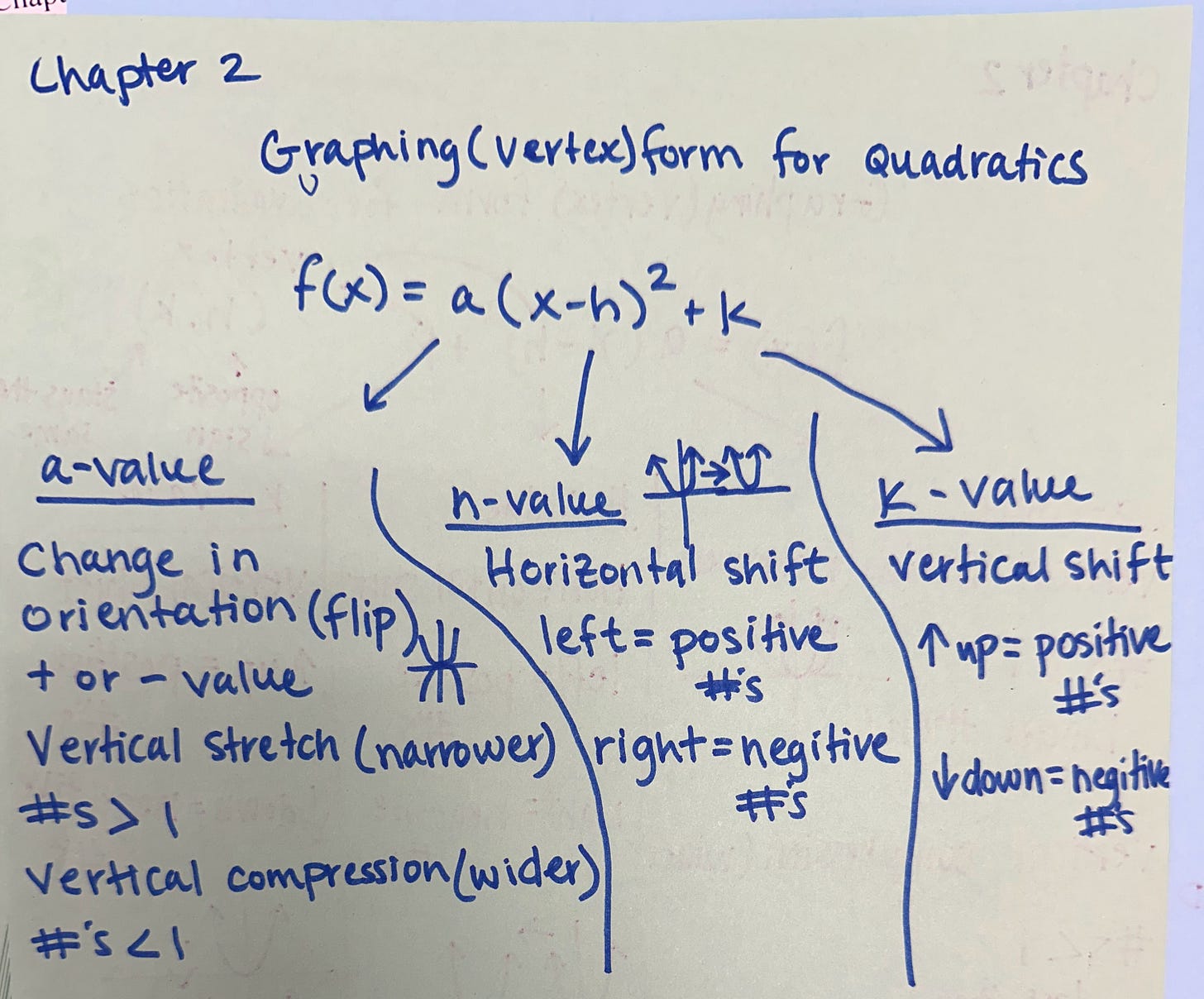
Direct instruction at the end of the lesson reinforces the concepts that I want my students to understand. I’ve noticed that my students will have wonderful discussions showing me that they understand the lesson goal, but don't feel confident that they have learned the concept until I work through an example in front of them.
It is important to note that since students have already worked through and solved multiple types of problems in groups, they only need me to work through one or two examples with them. Therefore, I have shortened the amount of time needed for direct instruction to the last few minutes of class.
As teachers we know that students need time and practice to let a concept sink in. To do this, I start class with a warm-up. This routine is one of the most important routines I have established and another chance for direct instruction. As students walk into my classroom, I have one or two questions displayed for them to start working on. I usually choose problems from previous lessons giving students the opportunity to check their understanding. After a few minutes of work time, students tell me how to solve the problems. This process fills any gaps that students might have in their understanding and catches up students who were absent. Even though this routine happens at the beginning of the class period, I wrote about it last because it really is a wrap up of previous lessons.
Warm-up time only includes problems that students have solved before and is never a time for “pre-teaching”. I mention this since it's easy to fall into the trap of pre-teaching during warm-ups. In my experience, the temptation to pre-teach is strong and often fueled by the desire to try to make the lesson run smoothly by eliminating the amount students struggle with solving the problems. But productive struggle is part of dialogic instruction and one of the reasons dialogic instruction yields a high effect size. If I pre-teach a concept, then I eliminate the dialogic part of the lesson and thinking problems turn into practice problems.
I also want to mention that warm-ups can be a time sucker, so it is important to keep them short and watch the time. I plan to write more about how I run warm-ups in a future post.
Lastly, there are times when I take the reins and do more of the talking during the direct instruction time. This is done mainly to save time. While I prefer to have students do the talking, I believe it is ok for me to explain problems if I know my students have first solved or tried to solve the problems on their own.
Munter, C., Stein, M.K., & Smith, M.S. (2015b). Is there a common pedagogical core? Examining instructional practices of competing models of mathematics teaching. NCSM Journal of Mathematics Education Leadership. 16(2), 3-13.
Hattie, John, Douglas Fisher, and Nancy Frey. 2017. Visible Learning for Mathematics. Thousand Oaks, CA: Corwin.







Finding that "sweet spot" of teacher-talk vs. student-talk takes time and experience, and you have articulated that very well. It's crucial that beginning teachers (and veterans as well!) don't get discouraged when they realize they have fallen back into old habits. Regroup, recommit, and keep on honing skills, good advice for both students and instructors.