Digital Interactives: Do They Inspire Thinking?

In my recent articles, White Boards versus Chromebooks and Are Digital Tools Cultivating Thinking? I talk about using digital interactives as thinking tasks. Everyday, teachers assign a multitude of tasks, and not all inspire thinking. The same is true for digital interactives. A digital interactive is a form of media where the user can engage with content which impacts the experience. There are so many digital interactives for teachers to choose from, it is important to be able to determine whether a digital interactive truly inspires thinking.

In Peter Liljedahl’s book, Building Thinking Classrooms in Mathematics, he describes scripted thinking tasks.

• Begin by asking a question about prior knowledge.

• Then ask a question that is an extension of that prior knowledge.

• Then ask students to do something without telling them what to do.

I might also add that a digital interactive inspires thinking when students are required to do something, an action, and think about the relationship between that action and its consequence.

Sometimes, I assign a single interactive or several interactives put together to form a digital lesson. In the digital lesson, Adding Integers Splat! there are many interactive slides. Let’s focus on a few slides with interactives that are meant to draw out students’ thinking about adding integers.

---

Begin by asking a question about prior knowledge.

On this slide students use their prior knowledge of two numbers that together make six. They may not choose correctly on the first try and that is okay. The interactive uses arrows and a boot as feedback to let the students determine if they were successful or not. Students use the feedback to adjust their answer, making a connection between the interactive and addition by writing a number sentence. This process allows all students to engage with the interactive and the math in an interesting way.

---

Then ask a question that is an extension of that prior knowledge.

The next two slides extend thinking about what happens when one of the numbers is negative. Students are new to adding negative numbers. They have seen that a negative number can be represented by an arrow pointing left on the number line which may help them choose the numbers. At this point students should start to make connections about the directions of the arrows and that adding positive and negative numbers acts a lot like subtraction.

---

Then ask students to do something without telling them what to do.

Finally, students try to find many different ways to add two numbers together to get the same result. By doing this, students start to develop their own understanding of what happens when they add two integers, which they formalize on the next slide.

After students have explained their thinking, the teacher has the opportunity to use students’ answers to drive a discussion about the algorithm for adding integers. Meaning, the students will tell the teacher how to add integers instead of the teacher telling the students. There is power in having students make their own connections between a math model and the algorithm, showing that these digital interactives inspired thinking.

Now that students know the algorithm for adding integers, the number line interactive is no longer needed and phased out as students practice their new knowledge. I think it is important to point out that the digital interactives did not show students how to add integers and did check their answers by stating correctness. All feedback was interpretive and allowed students to decide the path to a correct result.

In this article, Mitchel Resnick, a professor at MIT, says that for technology to be an effective teaching and learning tool it must have three qualities.

1. It has a low floor

2. It has wide walls

3. It has a high ceiling

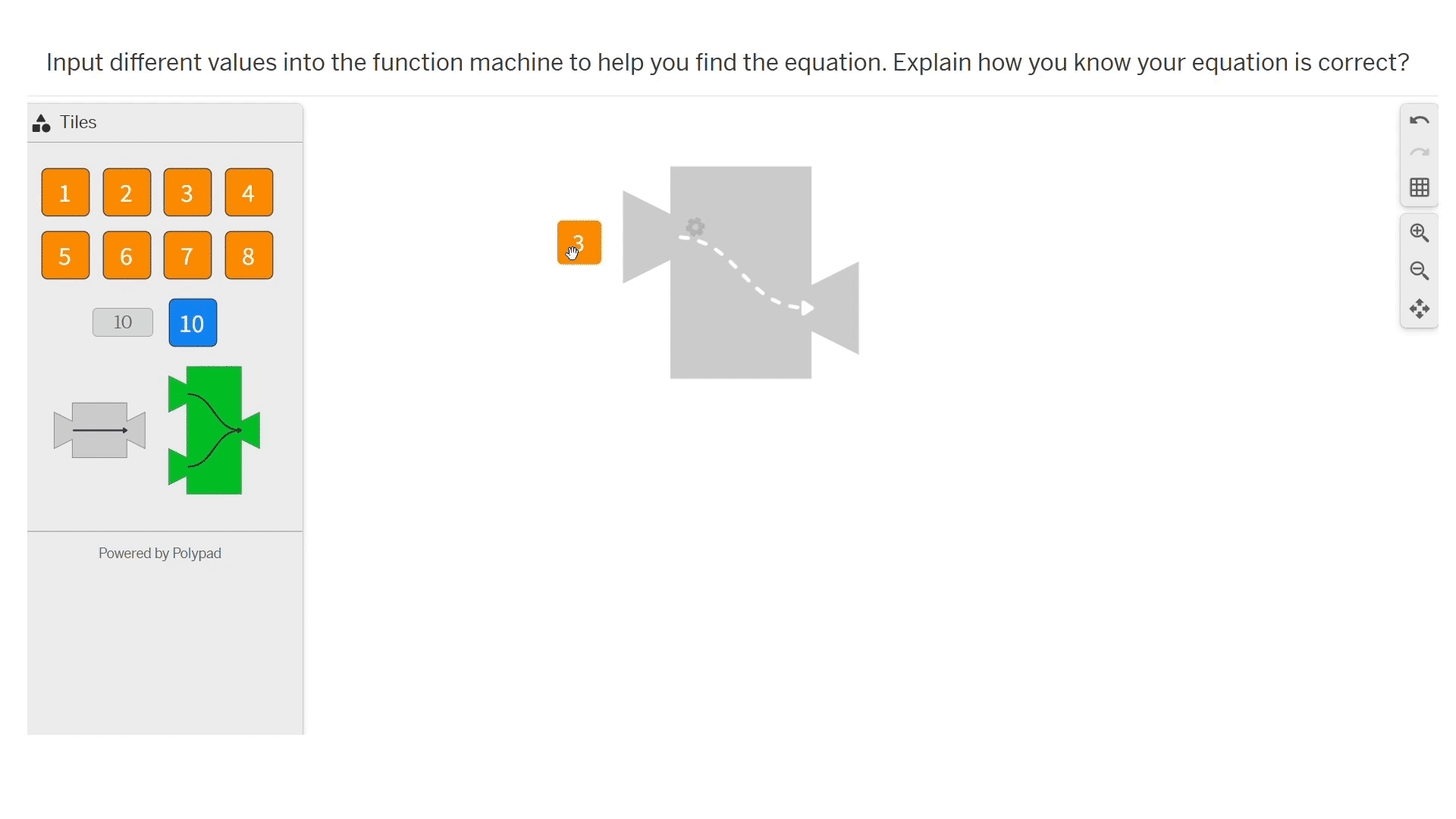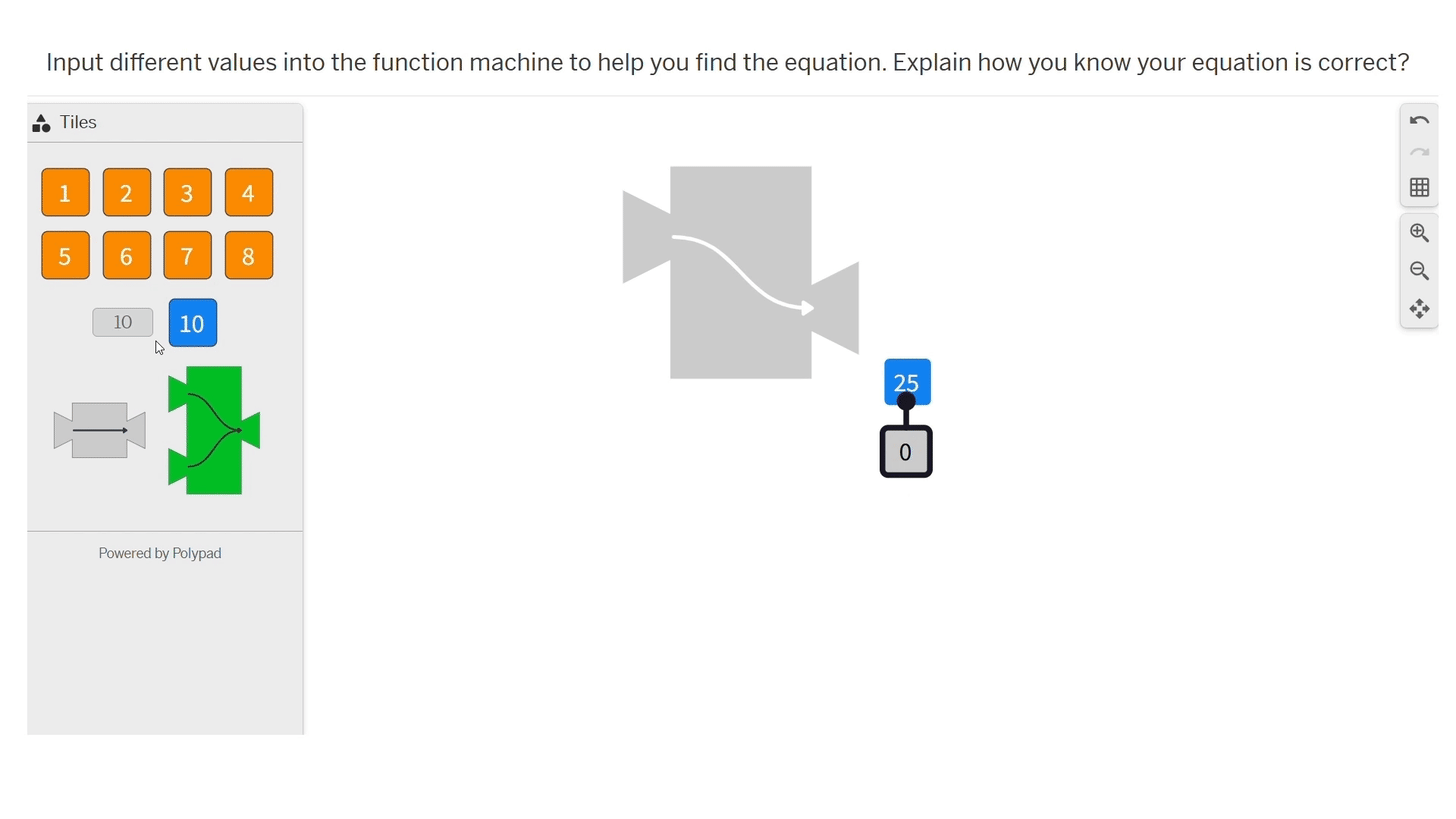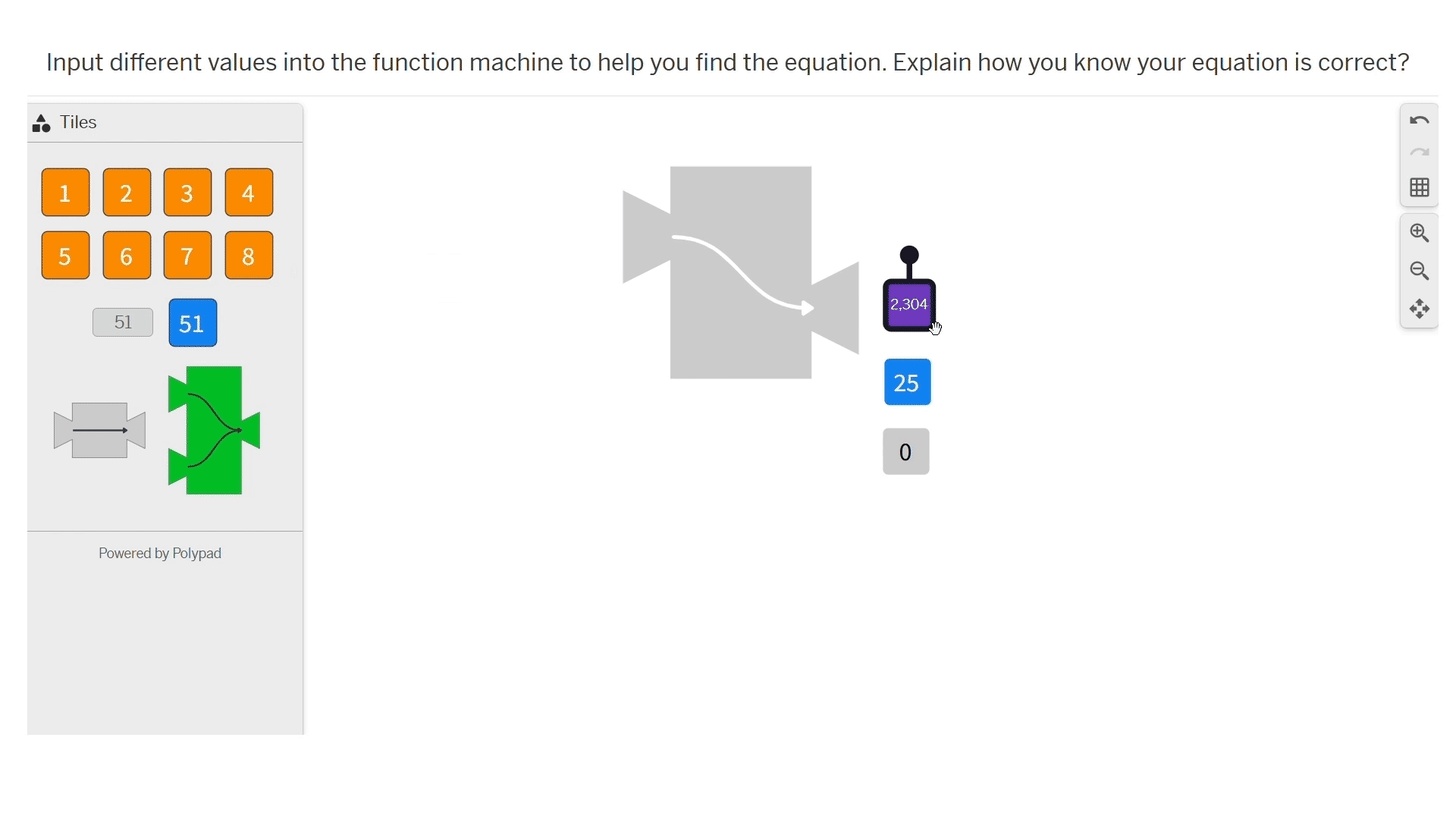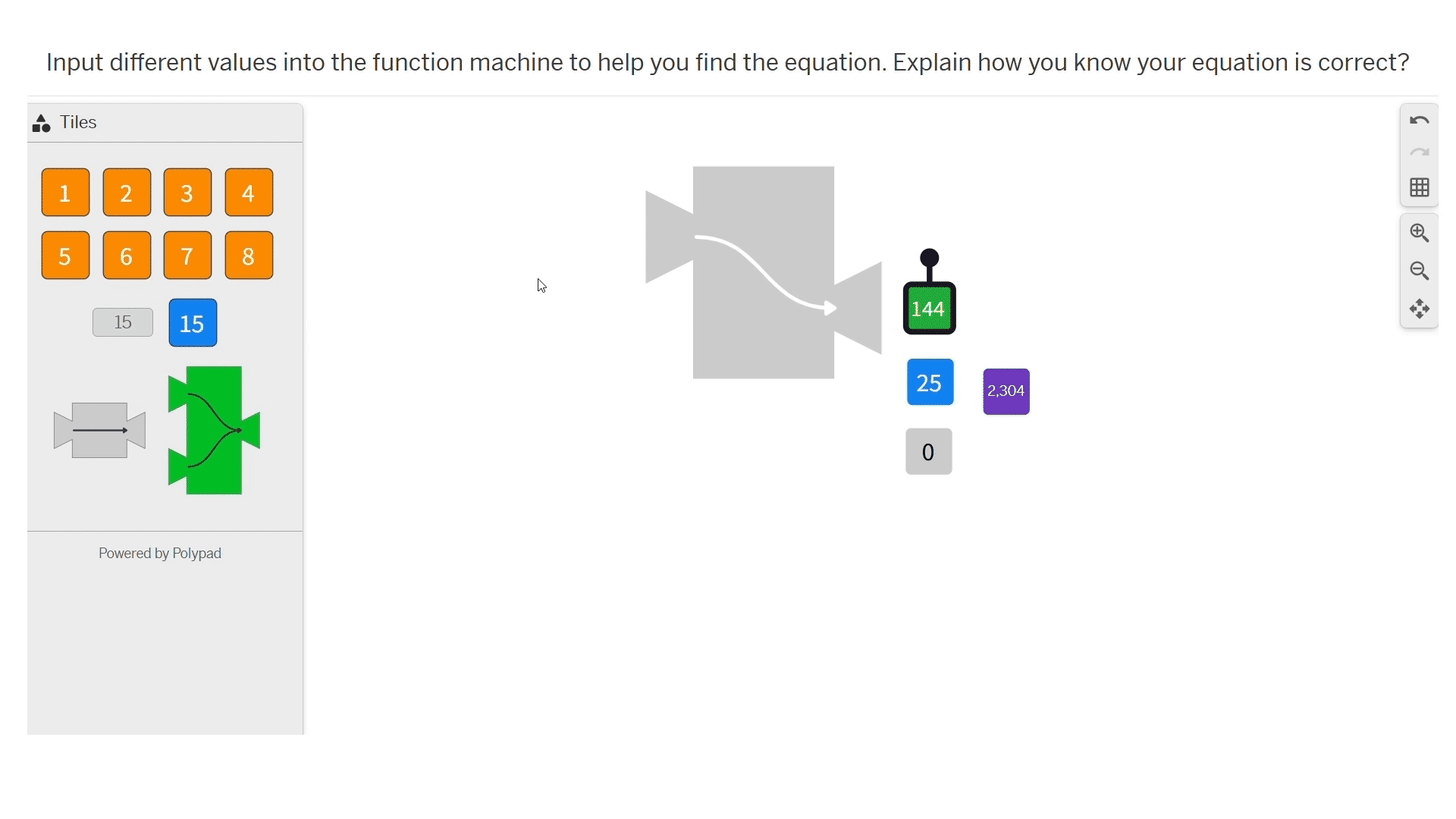
In the next interactive, students choose numbers to input into a function machine that generates output by applying an unknown function. Students are tasked with identifying the function.

Low floor.

Every student can engage with the interactive. Placing numbers into the function machine is exciting for students. They like seeing the numbers go in and come out.

Wide walls.

Usually, when students are learning about writing function equations they are given the input and output in the form of a table, graph, or context. The interactive is an interesting and different way to present the information. There is no guide for students on how to navigate the problem so they are allowed to choose their own path to explore the math.

High ceiling

Note: This is the work of teachers at a PD session.

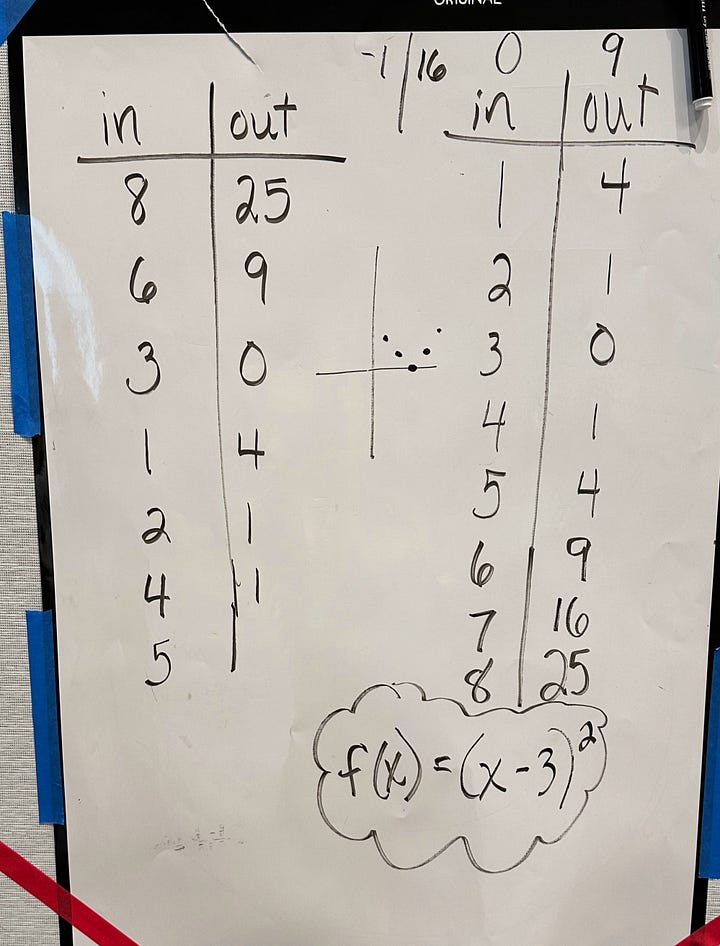
Students choose how to organize the input and output and look for patterns. Some students make tables and find the first and second differences or notice that the output numbers are perfect squares. Students may choose to graph the relationship and notice that the graph is a parabola or think about what they know about quadratic equations.

Not all digital interactives inspire thinking. While it is easy for all students to engage with this interactive, it tells the user why the relation is or isn’t a function, taking away the opportunity for students to think.

To make this interactive inspire thinking, I would change the feedback to only tell the students if the relation is a function or not. Then after several examples, students should be able to develop a conjecture about the definition of a function and test out their thoughts. I would then lead a discussion about the students’ thoughts and formalize a definition as a class.

Here are a few places I look to find digital interactives:

Desmos Classroom

GeoGebra (Be careful there are also many non-thinking tasks as I pointed out.)

Tim Brzezinski

Steve Phelps

SolveMe puzzles

David Poras

Good luck!! I hope both you and your students enjoy thinking with digital interactives!